TEACHING LARGE MODELS TO REASON ABOUT CAUSE AND EFFCTS
Reasoning is the emergent capability that allows large models to go beyond statistical pattern recognition in the training set. Among different types of reasoning skills, causal reasoning is fundamental for building generalizable and robust AI (in fact, it is necessary and sufficient for generalization, as proved in [1]). Therefore, we aim to answer the following questions:
- How to formally define causal reasoning in large models?
- Is it possible to build/teach large models that can consistenty perform such causal reasoning?
To address those questions, we must isolate the model’s pure causal reasoning capability from its common sense/knowledge extraction capabilities. This is done by defining causal reasoning as a form of inductive reasoning, aiming at outputing precise, quantitative causal hypothesis, given some measurement dataset sampled from any system as inputs (Fig. 1)

One example of causal reasoning problem is the classical structural causal learning problem (Fig. 2), where:
- The input (observation) is given by historical data measurement points; for example, some time series of health monitoring data.
- The output (causal hypothesis) is defined as the underlying causal structure between variables (i.e., which causes which); as well as the functional relationships (how much is the impact) .
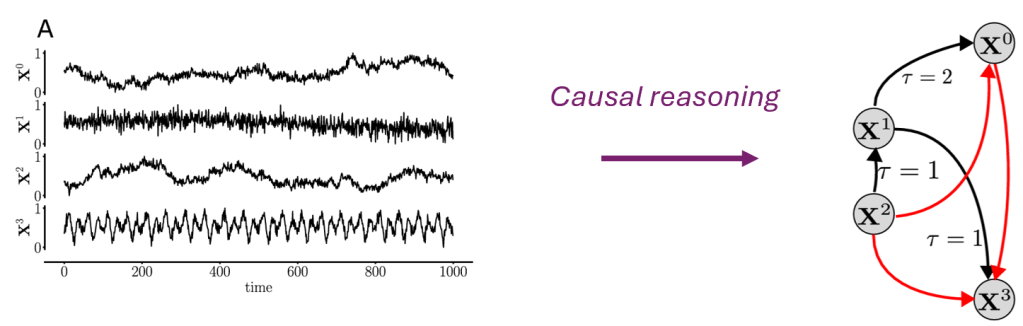
In this definition of causal reasoning, there are few important remarks:
- No prior common sense/domain knowledge is provided to the model; and the model is forced to figure out the underlying causal hypothesis solely based on observation evidence. In this controlled setting, the pure causal reasoning capability can therefore be studied.
- Our definition permits the discovery of new knowledge/new causal hypothesis, if novel evidence are provided to the model. Therefore, it steps away from the comfort zone of native LLMs, and might requires new modelling methods.
A naive way of teaching the model to perform causal reasoning is by showing it with a sufficient amount of {observation evidence, causal hypothesis} pairs, which is learnable via next token prediction. However, in most cases the true causal hypothesis is unknown, which makes learning to reason causally very challenging.
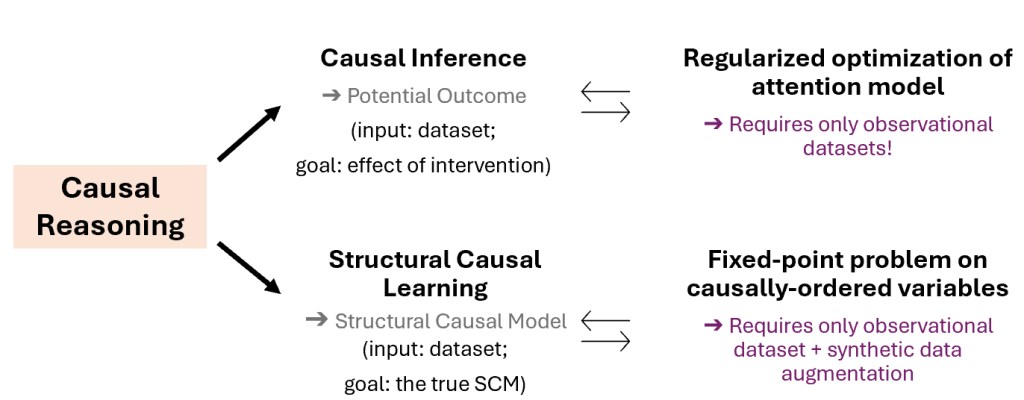
In our two ICML 2024 papers [2, 3], we proved that it is theoretically possible to reformulate causal reasoning questions as (mathematically-equivalent) self-supervised learning problems, that can be exactly mapped to existing next-token prediction architectures (e.g., transformers). Specifically (Fig. 3):
- For causal inference problems, we proved that it is possible to be reformulated as optimization problems of regularized attention model applied on observation dataset [2]. In fact, the necessary causal quantities needed for causal reasoning will be exactly stored in the value tensor of the attention module.
- The equivalent attention optimization problem only requires access to observational dataset/evidence during training. Interestingly, we have shown that in this setting, causal reasoning is in fact done in the post-training regime.
- For structural causal learning problems, we proved that they can be reformulated as a type of fixed point learning problem on causally-ordered tokens[3]. The latter problem is learnable by a specific type of attention architecture.
- This only requires observational dataset, plus some augmentation of with synthetic data.
In our empirical studies under controlled settings, we have found that if we train our model by solving the equivalent next-token-prediction problem , then they gain competitive causal reasoning capabilities. More importantly, such capabilities generalize well to unseen evidence from unseen systems. This validates our theoretical findings that causal reasoning is learnable via self-supervised training on observational data/evidence.
Reference:
[1] Robust agents learn causal world models. Jonathan Richens, Tom Everitt, ICLR 2024.
[2] Towards Causal Foundation Model: on Duality between Causal Inference and Attention, Jiaqi Zhang*, Joel Jennings, Agrin Hilmkil, Nick Pawlowski, Cheng Zhang, Chao Ma*. ICML 2024
[3] FiP: a Fixed-Point Approach for Causal Generative Modeling. Meyer Scetbon, Joel Jennings, Agrin Hilmkil, Cheng Zhang, Chao Ma, ICML 2024
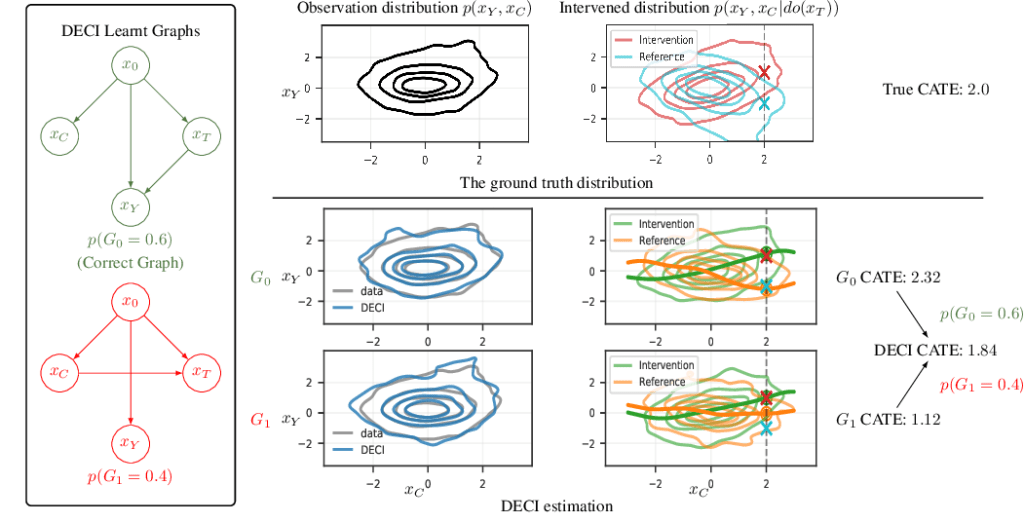
[2021-2023] DEEP END-TO-END CAUSAL INFERENCE
Causal machine learning is the key to enable individuals and organizations to make better data-driven decisions. In particular, causal ML allows us to answer “what if” questions about the effect of potential actions on outcomes.
Causal ML is a nascent area, we aim to enable a scalable, flexible, real-world applicable end-to-end causal inference framework. In perticular, we bridge between causal discovery, causal inference, and deep learning to achieve the goal. We aim to develop technology can automate causal decision-making using existing observational data alone, output both the discovered causal relationships and estimate the effect of actions simultaneously.
Recent Publications:
Deep End-to-end Causal Inference. Tomas Geffner, Javier Antoran, Adam Foster, Wenbo Gong, Chao Ma, Emre Kiciman, Amit Sharma, Angus Lamb, Martin Kukla, Nick Pawlowski, Miltiadis Allamanis, Cheng Zhang, NeurIPS 2022 Workshop on Causality for Real-world Impact
Causal Reasoning in the Presence of Latent Confounders via Neural ADMG Learning, Matthew Ashman*, Chao Ma*, Agrin Hilmkil, Joel Jennings, Cheng Zhang, ICLR 2023
A Causal AI Suite for Decision-Making, Emre Kiciman, Eleanor Wiske Dillon, Darren Edge, Adam Foster, Joel Jennings, Chao Ma, Robert Ness, Nick Pawlowski, Amit Sharma, Cheng Zhang, NeurIPS 2022 Workshop on Causality for Real-world Impact

[2018-2021] IMPLICIT STOCHASTIC PROCESSES, AND FUNCTION SPACE INFERENCE
Many supervised learning techniques in modern ML rely on i.i.d. assumptions of training data points gathered from the system of interest. On the contrary, Bayesian Nonparametric methods (BNs) generalized this assumption by defining priors over prediction functions (i.e., the stochastic processes), which induces exchangeable priors over data points. This introduces correlations between data points, and the prediction tasks can be viewed as the Bayesian inference problem in function space.
One famous example (and perhaps the mostly used BN approach in ML) is the Gaussian Processes (GPs). This approach has proven to be able to provide relatively accurate and reliable uncertainty estimates on unseen data, which is crucial for real-world applications. However, GPs suffers from limited scalability and expressiveness, which limit the applications of GPs. Inspired by recent advances in implicit models, I tried to take advantage of implicit models to construct stochastic processes that are more expressive to GPs. Similar to the construction of Gaussian processes (GPs), we can assign implicit distributions over any finite collections of random variables. Then, similar to Bayesian non-parameterics, one can directly perform Bayesian inference in function space. Such models are called implicit processes (IP). IPs brings together the best of both worlds, that is, combining the elegance of inference, and the well-calibrated uncertainty of Bayesian nonparametric methods, with the strong representational power of implicit models.
The main difficulty for applying this function-space view point to practical ML problems is that, IPs generally does not have simple analytic solutions for Bayesian inference. The paper titled “Variational Implicit Processes (VIP)” was our initial attempt at solving this problem. We derived a novel and efficient function space inference pipeline for such implicit processes, that gives a closed-form approximation to the IP posterior. For applications, we successfully applied our method to the problem of function space Bayesian inference for complicated IP priors. Click here for more information.
In the VIP paper, we discovered that the function space inference method applied to parameteric models (such as BNNs, Bayesian LSTMs, and dynamic systems) is very useful, and it often outperforms weight space VI methods. In line with the function-space perspective provided by VIP, we further investigate function space variational inference methods for general stochastic processes, that are more principled, accurate, and scalable.
Relevant publications:
Variational Implicit Processes Chao Ma, Yingzhen Li, and José Miguel Hernández-Lobato. Proceedings of the 36th International Conference on Machine Learning, 2019.
Functional Variational Inference for Stochastic Processes Chao Ma, José Miguel Hernández-Lobato. Advances in Neural Information Processing Systems, 2024.

[2018-2021] DATA EFFICIENT MACHINE LEARNING
State of the art modern AI algorithms often rely on the power of large datasets. One the contrary, Bayesian methods are often considered to be able to handle small-data regime much better. How about the gap in-between these two extreme situations? For example, human experts are often able to: 1, possess exaustive domain knowledge, 2, dynamically acquire new information based on the current understanding of the situation, and 3, make effective decisions given such limited information. Imagine a person walking into a hospital with a broken arm. The first question from health-care personnel would likely be “How did you break you arm?” instead of “Do you have a cold?”, because the answer reveals relevant information for this patient’s treatment.
Automating this human expertise of asking relevant questions is the key towards data efficient machine learning and decision making. However, in many real-world applications it is extremely difficult. In this research, we use Bayesian deep learning methods and expermental design to build powerful models and achieve optimal trade-offs.
Relevant publications:
EDDI: Efficient Dynamic Discovery of High-value Information with Partial VAEChao Ma, Sebastian Tschiatschek, Konstantina Palla, José Miguel Hernández-Lobato, Sebastian Nowozin, and Cheng Zhang. Proceedings of the 36th International Conference on Machine Learning, 2019.
FIT: a Fast and Accurate Framework for Solving Medical Inquiring and Diagnosing Tasks Weijie He, Xiaohao Mao, Chao Ma, José Miguel Hernández-Lobato, and Ting Chen. submitted, 2020
Bayesian EDDI: Sequential Variable Selection with Bayesian Partial VAE Chao Ma*, Wenbo Gong*, Sebastian Tschiatschek, Sebastian Nowozin, José Miguel Hernández-Lobato, and Cheng Zhang. Real-world Sequential Decision Making workshop, International Conference on Machine Learning, 2019.

[2018-2020] GENERATIVE MODELS FOR TABULAR DATA
Deep generative models often perform poorly in real-world applications due to the heterogeneity of natural data sets. Heterogeneity arises from data containing different types of features (categorical, ordinal, continuous, etc.) and features of the same type having different marginal distributions. We propose an extension of variational autoencoders (VAEs) called VAEM to handle such heterogeneous data. VAEM is a deep generative model that is trained in a two stage manner such that the first stage provides a more uniform representation of the data to the second stage, thereby sidestepping the problems caused by heterogeneous data. We provide extensions of VAEM to handle partially observed data, and demonstrate its performance in data generation, missing data prediction and sequential feature selection tasks. Our results show that VAEM broadens the range of real-world applications where deep generative models can be successfully deployed.
Revelent Publications
VAEM: a Deep Generative Model for Heterogeneous Mixed Type Data Chao Ma, Sebastian Tschiatschek, Richard Turner, José Miguel Hernández-Lobato, and Cheng Zhang. Advances in Neural Information Processing Systems, 2020.
HM-VAEs: a Deep Generative Model for Real-valued Data with Heterogeneous Marginals Chao Ma, Sebastian Tschiatschek, Yingzhen Li, Richard Turner, José Miguel Hernández-Lobato, and Cheng Zhang. Proceedings of The 2nd Symposium on Advances in Approximate Bayesian Inference, 2020.
Partial VAE for Hybrid Recommender System Chao Ma*, Wenbo Gong*, José Miguel Hernández-Lobato, Noam Koenigstein, Sebastian Nowozin, and Cheng Zhang. Neural Information Processing Systems Workshop on Bayesian Deep Learning, 2018.